On limitations of uniplex networks for modeling multiplex contagion
My paper with jimi adams, “On limitations of uniplex networks for modeling multiplex contagion” was published in PLoS ONE (Preprint here)! A thread by jimi:
Some years ago, I noticed an apparent growing trend of increasing precision, about (narrower?) behaviors/relationships in network data collection, (especially in studies of STIs - e.g., studies of sex OR needle sharing). Yet, when writing my “little green book” on network data collection (https://us.sagepub.com/en-us/nam/gathering-social-network-data/book260973), I became more and more intrigued by the fact that social network analysis initially was very multiplex in focus, and the focus on single ties at a time really came later.
I definitely think there are benefits to this focus (e.g., the need for domain expertise to improve data quality, etc.). But I also recognize that some of the ways such data are used don’t always consistently matchup to the theoretical topics of interest. The aim was to demonstrate when this “decomposed” data approach “adds up” to the full process of interest, and when it does not. But, I had way too many irons in the fire, so I back-burnered the idea, hoping to loop back at some point.
After encountering a talk & paper by @nwlandry I thought we could make my paper idea happen. I reached out to see if he’d be interested. He was, and took the lead from there.
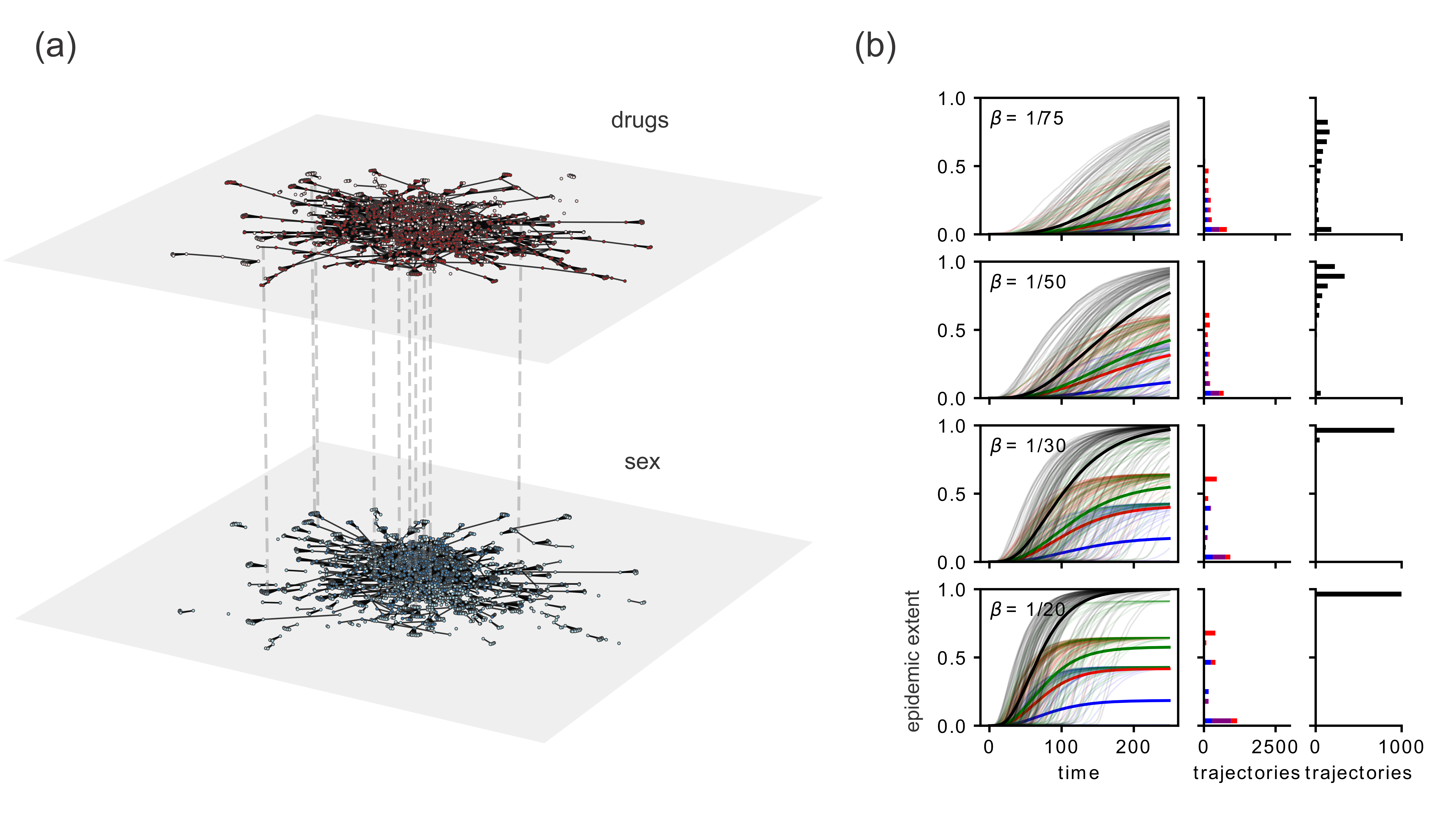
So the paper 1. takes a multiplex network & simulates a diffusion process over it, then 2. decomposes that network into its uniplex layers & runs a diffusion process over each of those separately, then 3. compares the union of simulations in (2) to the results in (1). [4/n]
Bottom line RQ: If we put these constituent pieces (as are available from studies of each tie type separately) back together, do we “recover” the full diffusion extent?”
We do this separately for 1. a behavioral network w/ a “simple” contagion process (i.e., an STI), and 2. an (online) social network for a “complex” contagion process (i.e., “an idea”). (Here, think of studying ideas spreading, but focusing on a single platform at a time.)
We find that combining the results from the 2 uniplex network contagion processes doesn’t align w/ their respective multiplex networks. In the simple contagion, the union epidemic extent is LESS than for the corresponding multiplex network. In the complex contagion, the union diffusion extent is GREATER than for the corresponding multiplex network. I see the big takeaway as we should reconsider whether this focus on data precision is an appropriate tradeoff for our theoretical aims.
Code & links to obtain data used are available here. Thanks again to @nwlandry for pulling this out of my “file drawer” and leading it to the light of day.