Polarization in hypergraphs with community structure

An illustration of a 3-uniform hypergraph sampled from the HPPM model with varying strengths of community structure using XGI.

I’m excited to belatedly announce that “Polarization in hypergraphs with community structure”, a collaboration with Juan G. Restrepo, is on arXiv! This project started almost by accident. We wanted to see whether community structure was affecting the epidemic threshold or the onset of tipping point behavior for the hypergraph SIS model. In our investigation, we found a very interesting phase diagram.

A phase plot of the mean-field equations with \epsilon_2 = 0.5, \widetilde{\beta}_2 = 0.2, and \widetilde{\beta}_3 = 4 for three different values of \widetilde{\epsilon}_3. These plots illustrate the cases where there are no asymmetric fixed points (\epsilon_3=0.75), only unstable asymmetric fixed points (\epsilon_3=0.85), and stable asymmetric fixed points (\epsilon_3=0.95). The filled circles correspond to stable fixed points and the open circles correspond to unstable fixed points.

This phase diagram shows that two different communities can have very different stable equilibria for strong enough community structure and we defined the “polarization” as the maximum distance between two communities’ stable fixed points. We investigated the infectious and structural parameters for which polarization exists. We concluded that polarization occurs below the epidemic threshold for sufficient higher-order infectiousness and is very sensitive to higher-order community structure.

The polarization with respect to community structure (first row) and infectiousness (second row). Note the different ranges of \epsilon_2 and \epsilon_3 in panels (a) and (b) and \widetilde{\beta}_2 and \widetilde{\beta}_3 in panels (c) and (d). The polarization is computed in two ways: from the stable fixed points of Eqs.~- (first column) and from stochastic simulations of the contagion dynamics (second column).

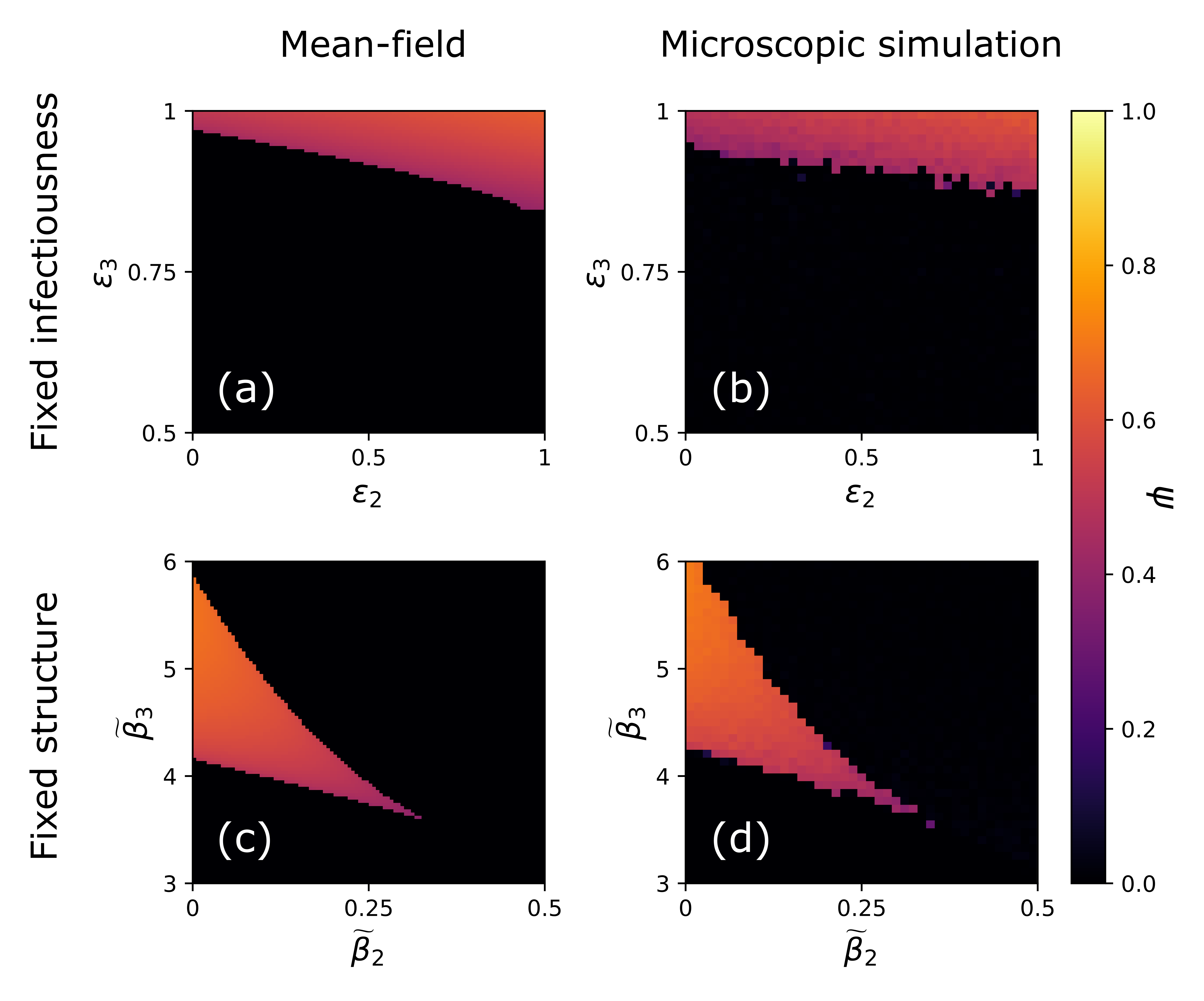
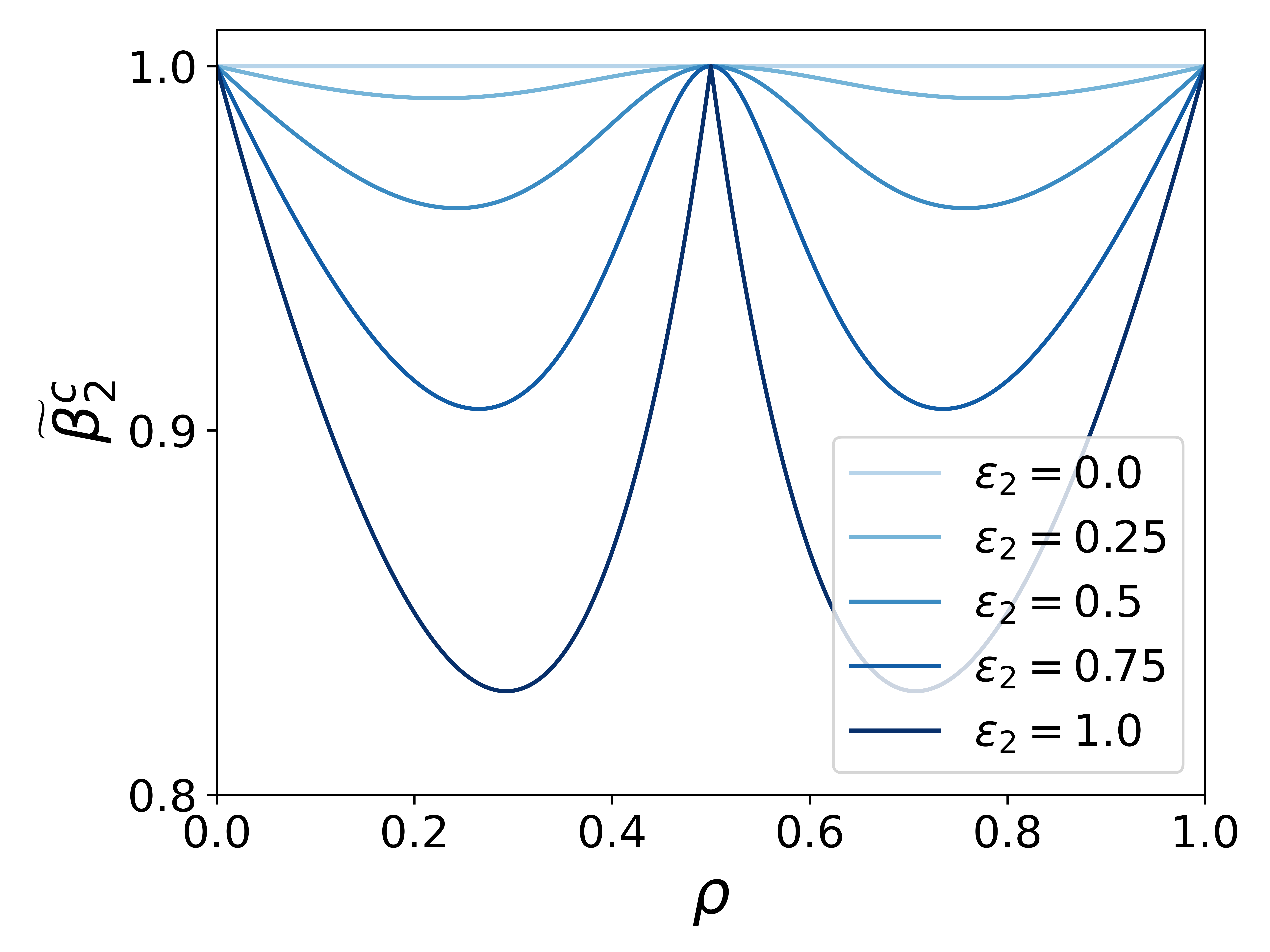
You can view the phenomenon of polarization as a perturbation of two completely disconnected communities, both in a bistable regime. We can see this by the shrinking region of polarization. This phenomenon may be a potential mechanism for the reinforcement of polarization, but is certainly not strong enough to spontaneously create polarization in a social system.

A phase diagram illustrating how changes with (a) \epsilon_2 and (b) \epsilon_3 affect the regions over which polarization can occur. In these diagrams, the upper left region enclosed by each line corresponds to the \widetilde{\beta}_2,\widetilde{\beta}_3 region in which polarization can occur for given values of \epsilon_2 and \epsilon_3, and the remaining area is where polarization does not occur. The boundary lines in panel (a) correspond to \epsilon_2 = 0, 0.25,0.5,0.75,1.0 with \epsilon_3 = 1 and the boundary lines in panel (b) correspond to \epsilon_3=0.95,0.9675,0.975,0.9875,1.0 with \epsilon_2 = 1.

Polarization (and the epidemic threshold, as seen below) is VERY sensitive to unequal community sizes. The phase plot becomes asymmetric and it matters which community holds which opinion. For a large enough disparity in community sizes, certain opinion configurations become untenable.

A plot of the epidemic threshold \widetilde{\beta}_2^c with respect to \rho predicted with the mean field equations. The line corresponding to \epsilon_2=0 is the epidemic threshold for the case.

A significant contribution in this paper is the development of fast algorithms to sample a modification of the hypergraph stochastic block model (HSBM) and the hypergraph Erdös-Rényi models. This is also the first project that I used XGI in earnest and it made the data management, analysis, and visualization SO much easier. Of course I’m biased, but I highly recommend trying it. Feel free to reach out if you have any ideas or suggestions!